Provides a simple and intuitive pipe-friendly framework, coherent with the ‘tidyverse’ design philosophy, for performing basic statistical tests, including t-test, Wilcoxon test, ANOVA, Kruskal-Wallis and correlation analyses.
The output of each test is automatically transformed into a tidy data frame to facilitate visualization.
Additional functions are available for reshaping, reordering, manipulating and visualizing correlation matrix. Functions are also included to facilitate the analysis of factorial experiments, including purely ‘within-Ss’ designs (repeated measures), purely ‘between-Ss’ designs, and mixed ‘within-and-between-Ss’ designs.
It’s also possible to compute several effect size metrics, including “eta squared” for ANOVA, “Cohen’s d” for t-test and “Cramer’s V” for the association between categorical variables. The package contains helper functions for identifying univariate and multivariate outliers, assessing normality and homogeneity of variances.
Key functions
Descriptive statistics
-
get_summary_stats(): Compute summary statistics for one or multiple numeric variables. Can handle grouped data. -
freq_table(): Compute frequency table of categorical variables. -
get_mode(): Compute the mode of a vector, that is the most frequent values. -
identify_outliers(): Detect univariate outliers using boxplot methods. -
mahalanobis_distance(): Compute Mahalanobis Distance and Flag Multivariate Outliers. -
shapiro_test()andmshapiro_test(): Univariate and multivariate Shapiro-Wilk normality test.
Comparing means
-
t_test(): perform one-sample, two-sample and pairwise t-tests -
wilcox_test(): perform one-sample, two-sample and pairwise Wilcoxon tests -
sign_test(): perform sign test to determine whether there is a median difference between paired or matched observations. -
anova_test(): an easy-to-use wrapper aroundcar::Anova()to perform different types of ANOVA tests, including independent measures ANOVA, repeated measures ANOVA and mixed ANOVA. -
get_anova_test_table(): extract ANOVA table fromanova_test()results. Can apply sphericity correction automatically in the case of within-subject (repeated measures) designs. -
welch_anova_test(): Welch one-Way ANOVA test. A pipe-friendly wrapper around the base functionstats::oneway.test(). This is is an alternative to the standard one-way ANOVA in the situation where the homogeneity of variance assumption is violated. -
kruskal_test(): perform kruskal-wallis rank sum test -
friedman_test(): Provides a pipe-friendly framework to perform a Friedman rank sum test, which is the non-parametric alternative to the one-way repeated measures ANOVA test. -
get_comparisons(): Create a list of possible pairwise comparisons between groups. -
get_pvalue_position(): autocompute p-value positions for plotting significance using ggplot2.
Facilitating ANOVA computation in R
-
factorial_design(): build factorial design for easily computing ANOVA using thecar::Anova()function. This might be very useful for repeated measures ANOVA, which is hard to set up with thecarpackage. -
anova_summary(): Create beautiful summary tables of ANOVA test results obtained from eithercar::Anova()orstats::aov(). The results include ANOVA table, generalized effect size and some assumption checks, such as Mauchly’s test for sphericity in the case of repeated measures ANOVA.
Post-hoc analyses
-
tukey_hsd(): performs tukey post-hoc tests. Can handle different inputs formats: aov, lm, formula. -
dunn_test(): compute multiple pairwise comparisons following Kruskal-Wallis test. -
games_howell_test(): Performs Games-Howell test, which is used to compare all possible combinations of group differences when the assumption of homogeneity of variances is violated. -
emmeans_test(): pipe-friendly wrapper arroundemmeansfunction to perform pairwise comparisons of estimated marginal means. Useful for post-hoc analyses following up ANOVA/ANCOVA tests.
Comparing proportions
-
prop_test(),pairwise_prop_test()androw_wise_prop_test(). Performs one-sample and two-samples z-test of proportions. Wrappers around the R base functionprop.test()but have the advantage of performing pairwise and row-wise z-test of two proportions, the post-hoc tests following a significant chi-square test of homogeneity for 2xc and rx2 contingency tables. -
fisher_test(),pairwise_fisher_test()androw_wise_fisher_test(): Fisher’s exact test for count data. Wrappers around the R base functionfisher.test()but have the advantage of performing pairwise and row-wise fisher tests, the post-hoc tests following a significant chi-square test of homogeneity for 2xc and rx2 contingency tables. -
chisq_test(),pairwise_chisq_gof_test(),pairwise_chisq_test_against_p(): Performs chi-squared tests, including goodness-of-fit, homogeneity and independence tests. -
binom_test(),pairwise_binom_test(),pairwise_binom_test_against_p(): Performs exact binomial test and pairwise comparisons following a significant exact multinomial test. Alternative to the chi-square test of goodness-of-fit-test when the sample. -
multinom_test(): performs an exact multinomial test. Alternative to the chi-square test of goodness-of-fit-test when the sample size is small. -
mcnemar_test(): performs McNemar chi-squared test to compare paired proportions. Provides pairwise comparisons between multiple groups. -
cochran_qtest(): extension of the McNemar Chi-squared test for comparing more than two paired proportions. -
prop_trend_test(): Performs chi-squared test for trend in proportion. This test is also known as Cochran-Armitage trend test.
Comparing variances
-
levene_test(): Pipe-friendly framework to easily compute Levene’s test for homogeneity of variance across groups. Handles grouped data. -
box_m(): Box’s M-test for homogeneity of covariance matrices
Effect Size
-
cohens_d(): Compute cohen’s d measure of effect size for t-tests. -
wilcox_effsize(): Compute Wilcoxon effect size (r). -
eta_squared()andpartial_eta_squared(): Compute effect size for ANOVA. -
kruskal_effsize(): Compute the effect size for Kruskal-Wallis test as the eta squared based on the H-statistic. -
friedman_effsize(): Compute the effect size of Friedman test using the Kendall’s W value. -
cramer_v(): Compute Cramer’s V, which measures the strength of the association between categorical variables.
Correlation analysis
Computing correlation:
-
cor_test(): correlation test between two or more variables using Pearson, Spearman or Kendall methods. -
cor_mat(): compute correlation matrix with p-values. Returns a data frame containing the matrix of the correlation coefficients. The output has an attribute named “pvalue”, which contains the matrix of the correlation test p-values. -
cor_get_pval(): extract a correlation matrix p-values from an object of classcor_mat(). -
cor_pmat(): compute the correlation matrix, but returns only the p-values of the correlation tests. -
as_cor_mat(): convert acor_testobject into a correlation matrix format.
Reshaping correlation matrix:
-
cor_reorder(): reorder correlation matrix, according to the coefficients, using the hierarchical clustering method. -
cor_gather(): takes a correlation matrix and collapses (or melt) it into long format data frame (paired list) -
cor_spread(): spread a long correlation data frame into wide format (correlation matrix).
Subsetting correlation matrix:
-
cor_select(): subset a correlation matrix by selecting variables of interest. -
pull_triangle(),pull_upper_triangle(),pull_lower_triangle(): pull upper and lower triangular parts of a (correlation) matrix. -
replace_triangle(),replace_upper_triangle(),replace_lower_triangle(): replace upper and lower triangular parts of a (correlation) matrix.
Visualizing correlation matrix:
-
cor_as_symbols(): replaces the correlation coefficients, in a matrix, by symbols according to the value. -
cor_plot(): visualize correlation matrix using base plot. -
cor_mark_significant(): add significance levels to a correlation matrix.
Adjusting p-values, formatting and adding significance symbols
-
adjust_pvalue(): add an adjusted p-values column to a data frame containing statistical test p-values -
add_significance(): add a column containing the p-value significance level -
p_round(), p_format(), p_mark_significant(): rounding and formatting p-values
Extract information from statistical tests
Extract information from statistical test results. Useful for labelling plots with test outputs.
-
get_pwc_label(): Extract label from pairwise comparisons. -
get_test_label(): Extract label from statistical tests. -
create_test_label(): Create labels from user specified test results.
Data manipulation helper functions
These functions are internally used in the rstatix and in the ggpubr R package to make it easy to program with tidyverse packages using non standard evaluation.
-
df_select(),df_arrange(),df_group_by(): wrappers arround dplyr functions for supporting standard and non standard evaluations. -
df_nest_by(): Nest a tibble data frame using grouping specification. Supports standard and non standard evaluations. -
df_split_by(): Split a data frame by groups into subsets or data panel. Very similar to the functiondf_nest_by(). The only difference is that, it adds labels to each data subset. Labels are the combination of the grouping variable levels. -
df_unite(): Unite multiple columns into one. -
df_unite_factors(): Unite factor columns. First, order factors levels then merge them into one column. The output column is a factor. -
df_label_both(),df_label_value(): functions to label data frames rows by by one or multiple grouping variables. -
df_get_var_names(): Returns user specified variable names. Supports standard and non standard evaluation.
Others
-
doo(): alternative to dplyr::do for doing anything. Technically it usesnest() + mutate() + map()to apply arbitrary computation to a grouped data frame. -
sample_n_by(): sample n rows by group from a table -
convert_as_factor(), set_ref_level(), reorder_levels(): Provides pipe-friendly functions to convert simultaneously multiple variables into a factor variable. -
make_clean_names(): Pipe-friendly function to make syntactically valid column names (for input data frame) or names (for input vector). -
counts_to_cases(): converts a contingency table or a data frame of counts into a data frame of individual observations.
Installation and loading
- Install the latest developmental version from GitHub as follow:
if(!require(devtools)) install.packages("devtools")
devtools::install_github("kassambara/rstatix")- Or install from CRAN as follow:
install.packages("rstatix")- Loading packages
Descriptive statistics
# Summary statistics of some selected variables
#::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
iris %>%
get_summary_stats(Sepal.Length, Sepal.Width, type = "common")
#> # A tibble: 2 x 10
#> variable n min max median iqr mean sd se ci
#> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 Sepal.Length 150 4.3 7.9 5.8 1.3 5.84 0.828 0.068 0.134
#> 2 Sepal.Width 150 2 4.4 3 0.5 3.06 0.436 0.036 0.07
# Whole data frame
#::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
iris %>% get_summary_stats(type = "common")
#> # A tibble: 4 x 10
#> variable n min max median iqr mean sd se ci
#> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 Sepal.Length 150 4.3 7.9 5.8 1.3 5.84 0.828 0.068 0.134
#> 2 Sepal.Width 150 2 4.4 3 0.5 3.06 0.436 0.036 0.07
#> 3 Petal.Length 150 1 6.9 4.35 3.5 3.76 1.76 0.144 0.285
#> 4 Petal.Width 150 0.1 2.5 1.3 1.5 1.20 0.762 0.062 0.123
# Grouped data
#::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
iris %>%
group_by(Species) %>%
get_summary_stats(Sepal.Length, type = "mean_sd")
#> # A tibble: 3 x 5
#> Species variable n mean sd
#> <fct> <fct> <dbl> <dbl> <dbl>
#> 1 setosa Sepal.Length 50 5.01 0.352
#> 2 versicolor Sepal.Length 50 5.94 0.516
#> 3 virginica Sepal.Length 50 6.59 0.636Comparing two means
To compare the means of two groups, you can use either the function t_test() (parametric) or wilcox_test() (non-parametric). In the following example the t-test will be illustrated.
One-sample test
The one-sample test is used to compare the mean of one sample to a known standard (or theoretical / hypothetical) mean (mu).
df %>% t_test(len ~ 1, mu = 0)
#> # A tibble: 1 x 7
#> .y. group1 group2 n statistic df p
#> * <chr> <chr> <chr> <int> <dbl> <dbl> <dbl>
#> 1 len 1 null model 60 19.1 59 6.94e-27
# One-sample test of each dose level
df %>%
group_by(dose) %>%
t_test(len ~ 1, mu = 0)
#> # A tibble: 3 x 8
#> dose .y. group1 group2 n statistic df p
#> * <fct> <chr> <chr> <chr> <int> <dbl> <dbl> <dbl>
#> 1 0.5 len 1 null model 20 10.5 19 2.24e- 9
#> 2 1 len 1 null model 20 20.0 19 3.22e-14
#> 3 2 len 1 null model 20 30.9 19 1.03e-17Compare two independent groups
- Create a simple box plot with p-values:
# T-test
stat.test <- df %>%
t_test(len ~ supp, paired = FALSE)
stat.test
#> # A tibble: 1 x 8
#> .y. group1 group2 n1 n2 statistic df p
#> * <chr> <chr> <chr> <int> <int> <dbl> <dbl> <dbl>
#> 1 len OJ VC 30 30 1.92 55.3 0.0606
# Create a box plot
p <- ggboxplot(
df, x = "supp", y = "len",
color = "supp", palette = "jco", ylim = c(0,40)
)
# Add the p-value manually
p + stat_pvalue_manual(stat.test, label = "p", y.position = 35)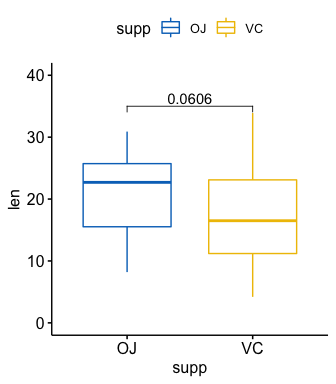
- Customize labels using glue expression:
p +stat_pvalue_manual(stat.test, label = "T-test, p = {p}",
y.position = 36)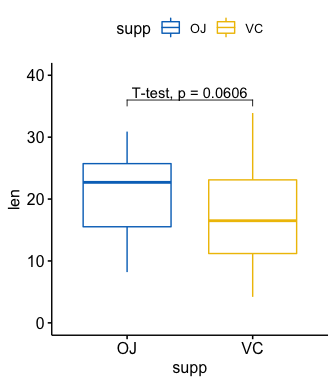
- Grouped data: compare supp levels after grouping the data by “dose”
# Statistical test
stat.test <- df %>%
group_by(dose) %>%
t_test(len ~ supp) %>%
adjust_pvalue() %>%
add_significance("p.adj")
stat.test
#> # A tibble: 3 x 11
#> dose .y. group1 group2 n1 n2 statistic df p p.adj
#> <fct> <chr> <chr> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl>
#> 1 0.5 len OJ VC 10 10 3.17 15.0 0.00636 0.0127
#> 2 1 len OJ VC 10 10 4.03 15.4 0.00104 0.00312
#> 3 2 len OJ VC 10 10 -0.0461 14.0 0.964 0.964
#> # … with 1 more variable: p.adj.signif <chr>
# Visualization
ggboxplot(
df, x = "supp", y = "len",
color = "supp", palette = "jco", facet.by = "dose",
ylim = c(0, 40)
) +
stat_pvalue_manual(stat.test, label = "p.adj", y.position = 35)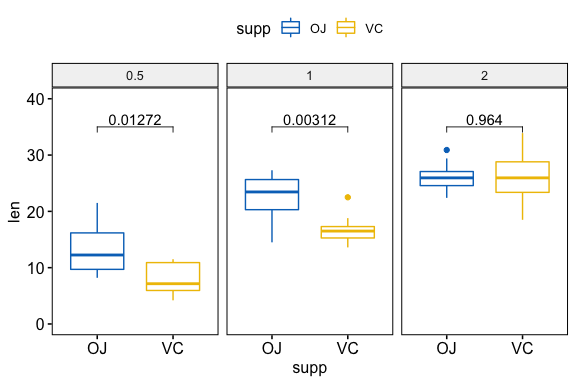
Compare paired samples
# T-test
stat.test <- df %>%
t_test(len ~ supp, paired = TRUE)
stat.test
#> # A tibble: 1 x 8
#> .y. group1 group2 n1 n2 statistic df p
#> * <chr> <chr> <chr> <int> <int> <dbl> <dbl> <dbl>
#> 1 len OJ VC 30 30 3.30 29 0.00255
# Box plot
p <- ggpaired(
df, x = "supp", y = "len", color = "supp", palette = "jco",
line.color = "gray", line.size = 0.4, ylim = c(0, 40)
)
p + stat_pvalue_manual(stat.test, label = "p", y.position = 36)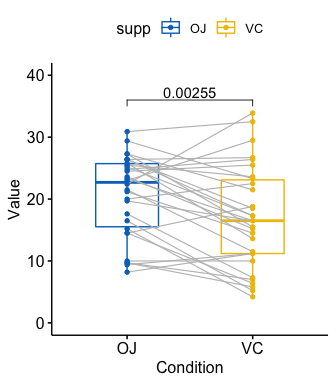
Multiple pairwise comparisons
- Pairwise comparisons: if the grouping variable contains more than two categories, a pairwise comparison is automatically performed.
# Pairwise t-test
pairwise.test <- df %>% t_test(len ~ dose)
pairwise.test
#> # A tibble: 3 x 10
#> .y. group1 group2 n1 n2 statistic df p p.adj p.adj.signif
#> * <chr> <chr> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <chr>
#> 1 len 0.5 1 20 20 -6.48 38.0 1.27e- 7 2.54e- 7 ****
#> 2 len 0.5 2 20 20 -11.8 36.9 4.40e-14 1.32e-13 ****
#> 3 len 1 2 20 20 -4.90 37.1 1.91e- 5 1.91e- 5 ****
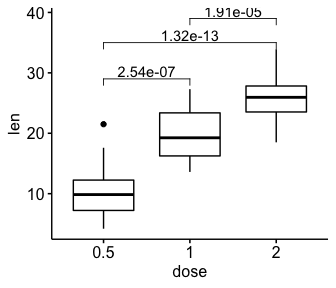
# Box plot
ggboxplot(df, x = "dose", y = "len")+
stat_pvalue_manual(
pairwise.test, label = "p.adj",
y.position = c(29, 35, 39)
)
- Multiple pairwise comparisons against reference group: each level is compared to the ref group
# Comparison against reference group
#::::::::::::::::::::::::::::::::::::::::
# T-test: each level is compared to the ref group
stat.test <- df %>% t_test(len ~ dose, ref.group = "0.5")
stat.test
#> # A tibble: 2 x 10
#> .y. group1 group2 n1 n2 statistic df p p.adj p.adj.signif
#> * <chr> <chr> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <chr>
#> 1 len 0.5 1 20 20 -6.48 38.0 1.27e- 7 1.27e- 7 ****
#> 2 len 0.5 2 20 20 -11.8 36.9 4.40e-14 8.80e-14 ****
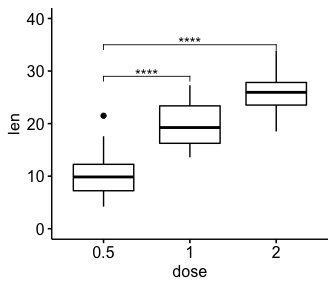
# Box plot
ggboxplot(df, x = "dose", y = "len", ylim = c(0, 40)) +
stat_pvalue_manual(
stat.test, label = "p.adj.signif",
y.position = c(29, 35)
)
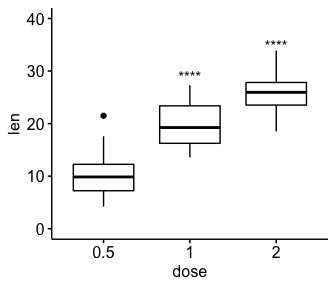
# Remove bracket
ggboxplot(df, x = "dose", y = "len", ylim = c(0, 40)) +
stat_pvalue_manual(
stat.test, label = "p.adj.signif",
y.position = c(29, 35),
remove.bracket = TRUE
)
- Multiple pairwise comparisons against all (base-mean): Comparison of each group against base-mean.
# T-test
stat.test <- df %>% t_test(len ~ dose, ref.group = "all")
stat.test
#> # A tibble: 3 x 10
#> .y. group1 group2 n1 n2 statistic df p p.adj p.adj.signif
#> * <chr> <chr> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <chr>
#> 1 len all 0.5 60 20 5.82 56.4 2.90e-7 8.70e-7 ****
#> 2 len all 1 60 20 -0.660 57.5 5.12e-1 5.12e-1 ns
#> 3 len all 2 60 20 -5.61 66.5 4.25e-7 8.70e-7 ****
# Box plot with horizontal mean line
ggboxplot(df, x = "dose", y = "len") +
stat_pvalue_manual(
stat.test, label = "p.adj.signif",
y.position = 35,
remove.bracket = TRUE
) +
geom_hline(yintercept = mean(df$len), linetype = 2)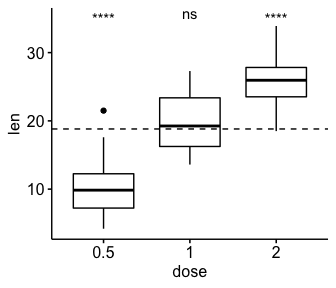
ANOVA test
# One-way ANOVA test
#:::::::::::::::::::::::::::::::::::::::::
df %>% anova_test(len ~ dose)
#> ANOVA Table (type II tests)
#>
#> Effect DFn DFd F p p<.05 ges
#> 1 dose 2 57 67.416 9.53e-16 * 0.703
# Two-way ANOVA test
#:::::::::::::::::::::::::::::::::::::::::
df %>% anova_test(len ~ supp*dose)
#> ANOVA Table (type II tests)
#>
#> Effect DFn DFd F p p<.05 ges
#> 1 supp 1 54 15.572 2.31e-04 * 0.224
#> 2 dose 2 54 92.000 4.05e-18 * 0.773
#> 3 supp:dose 2 54 4.107 2.20e-02 * 0.132
# Two-way repeated measures ANOVA
#:::::::::::::::::::::::::::::::::::::::::
df$id <- rep(1:10, 6) # Add individuals id
# Use formula
# df %>% anova_test(len ~ supp*dose + Error(id/(supp*dose)))
# or use character vector
df %>% anova_test(dv = len, wid = id, within = c(supp, dose))
#> ANOVA Table (type III tests)
#>
#> $ANOVA
#> Effect DFn DFd F p p<.05 ges
#> 1 supp 1 9 34.866 2.28e-04 * 0.224
#> 2 dose 2 18 106.470 1.06e-10 * 0.773
#> 3 supp:dose 2 18 2.534 1.07e-01 0.132
#>
#> $`Mauchly's Test for Sphericity`
#> Effect W p p<.05
#> 1 dose 0.807 0.425
#> 2 supp:dose 0.934 0.761
#>
#> $`Sphericity Corrections`
#> Effect GGe DF[GG] p[GG] p[GG]<.05 HFe DF[HF] p[HF]
#> 1 dose 0.838 1.68, 15.09 2.79e-09 * 1.008 2.02, 18.15 1.06e-10
#> 2 supp:dose 0.938 1.88, 16.88 1.12e-01 1.176 2.35, 21.17 1.07e-01
#> p[HF]<.05
#> 1 *
#> 2
# Use model as arguments
#:::::::::::::::::::::::::::::::::::::::::
.my.model <- lm(yield ~ block + N*P*K, npk)
anova_test(.my.model)
#> ANOVA Table (type II tests)
#>
#> Effect DFn DFd F p p<.05 ges
#> 1 block 4 12 4.959 0.014 * 0.623
#> 2 N 1 12 12.259 0.004 * 0.505
#> 3 P 1 12 0.544 0.475 0.043
#> 4 K 1 12 6.166 0.029 * 0.339
#> 5 N:P 1 12 1.378 0.263 0.103
#> 6 N:K 1 12 2.146 0.169 0.152
#> 7 P:K 1 12 0.031 0.863 0.003
#> 8 N:P:K 0 12 NA NA <NA> NACorrelation tests
# Data preparation
mydata <- mtcars %>%
select(mpg, disp, hp, drat, wt, qsec)
head(mydata, 3)
#> mpg disp hp drat wt qsec
#> Mazda RX4 21.0 160 110 3.90 2.620 16.46
#> Mazda RX4 Wag 21.0 160 110 3.90 2.875 17.02
#> Datsun 710 22.8 108 93 3.85 2.320 18.61
# Correlation test between two variables
mydata %>% cor_test(wt, mpg, method = "pearson")
#> # A tibble: 1 x 8
#> var1 var2 cor statistic p conf.low conf.high method
#> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>
#> 1 wt mpg -0.87 -9.56 1.29e-10 -0.934 -0.744 Pearson
# Correlation of one variable against all
mydata %>% cor_test(mpg, method = "pearson")
#> # A tibble: 5 x 8
#> var1 var2 cor statistic p conf.low conf.high method
#> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>
#> 1 mpg disp -0.85 -8.75 9.38e-10 -0.923 -0.708 Pearson
#> 2 mpg hp -0.78 -6.74 1.79e- 7 -0.885 -0.586 Pearson
#> 3 mpg drat 0.68 5.10 1.78e- 5 0.436 0.832 Pearson
#> 4 mpg wt -0.87 -9.56 1.29e-10 -0.934 -0.744 Pearson
#> 5 mpg qsec 0.42 2.53 1.71e- 2 0.0820 0.670 Pearson
# Pairwise correlation test between all variables
mydata %>% cor_test(method = "pearson")
#> # A tibble: 36 x 8
#> var1 var2 cor statistic p conf.low conf.high method
#> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>
#> 1 mpg mpg 1 Inf 0. 1 1 Pearson
#> 2 mpg disp -0.85 -8.75 9.38e-10 -0.923 -0.708 Pearson
#> 3 mpg hp -0.78 -6.74 1.79e- 7 -0.885 -0.586 Pearson
#> 4 mpg drat 0.68 5.10 1.78e- 5 0.436 0.832 Pearson
#> 5 mpg wt -0.87 -9.56 1.29e-10 -0.934 -0.744 Pearson
#> 6 mpg qsec 0.42 2.53 1.71e- 2 0.0820 0.670 Pearson
#> 7 disp mpg -0.85 -8.75 9.38e-10 -0.923 -0.708 Pearson
#> 8 disp disp 1 Inf 0. 1 1 Pearson
#> 9 disp hp 0.79 7.08 7.14e- 8 0.611 0.893 Pearson
#> 10 disp drat -0.71 -5.53 5.28e- 6 -0.849 -0.481 Pearson
#> # … with 26 more rowsCorrelation matrix
# Compute correlation matrix
#::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
cor.mat <- mydata %>% cor_mat()
cor.mat
#> # A tibble: 6 x 7
#> rowname mpg disp hp drat wt qsec
#> * <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 mpg 1 -0.85 -0.78 0.68 -0.87 0.42
#> 2 disp -0.85 1 0.79 -0.71 0.89 -0.43
#> 3 hp -0.78 0.79 1 -0.45 0.66 -0.71
#> 4 drat 0.68 -0.71 -0.45 1 -0.71 0.091
#> 5 wt -0.87 0.89 0.66 -0.71 1 -0.17
#> 6 qsec 0.42 -0.43 -0.71 0.091 -0.17 1
# Show the significance levels
#::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
cor.mat %>% cor_get_pval()
#> # A tibble: 6 x 7
#> rowname mpg disp hp drat wt qsec
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 mpg 0. 9.38e-10 0.000000179 0.0000178 1.29e- 10 0.0171
#> 2 disp 9.38e-10 0. 0.0000000714 0.00000528 1.22e- 11 0.0131
#> 3 hp 1.79e- 7 7.14e- 8 0 0.00999 4.15e- 5 0.00000577
#> 4 drat 1.78e- 5 5.28e- 6 0.00999 0 4.78e- 6 0.62
#> 5 wt 1.29e-10 1.22e-11 0.0000415 0.00000478 2.27e-236 0.339
#> 6 qsec 1.71e- 2 1.31e- 2 0.00000577 0.62 3.39e- 1 0
# Replacing correlation coefficients by symbols
#::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
cor.mat %>%
cor_as_symbols() %>%
pull_lower_triangle()
#> rowname mpg disp hp drat wt qsec
#> 1 mpg
#> 2 disp *
#> 3 hp * *
#> 4 drat + + .
#> 5 wt * * + +
#> 6 qsec . . +
# Mark significant correlations
#::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
cor.mat %>%
cor_mark_significant()
#> rowname mpg disp hp drat wt qsec
#> 1 mpg
#> 2 disp -0.85****
#> 3 hp -0.78**** 0.79****
#> 4 drat 0.68**** -0.71**** -0.45**
#> 5 wt -0.87**** 0.89**** 0.66**** -0.71****
#> 6 qsec 0.42* -0.43* -0.71**** 0.091 -0.17
# Draw correlogram using R base plot
#::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
cor.mat %>%
cor_reorder() %>%
pull_lower_triangle() %>%
cor_plot()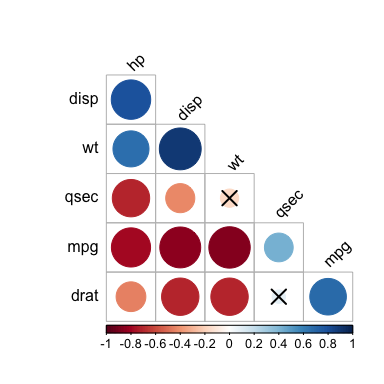
Related articles
- How to Add P-Values onto Basic GGPLOTS
- How to Add Adjusted P-values to a Multi-Panel GGPlot
- How to Add P-values to GGPLOT Facets
- How to Add P-Values Generated Elsewhere to a GGPLOT
- How to Add P-Values onto a Grouped GGPLOT using the GGPUBR R Package
- How to Create Stacked Bar Plots with Error Bars and P-values
- How to Add P-Values onto Horizontal GGPLOTS
- Add P-values and Significance Levels to ggplots
- Comparing Means of Two Groups in R
- Comparing Multiple Means in R