Hierarchical k-means clustering — hkmeans • factoextra

The final k-means clustering solution is very sensitive to the initial random selection of cluster centers. This function provides a solution using an hybrid approach by combining the hierarchical clustering and the k-means methods. The procedure is explained in "Details" section. Read more: Hybrid hierarchical k-means clustering for optimizing clustering outputs.

hkmeans(): compute hierarchical k-means clustering
print.hkmeans(): prints the result of hkmeans
hkmeans_tree(): plots the initial dendrogram

hkmeans(
  x,
  k,
  hc.metric = "euclidean",
  hc.method = "ward.D2",
  iter.max = 10,
  km.algorithm = "Hartigan-Wong"
)

# S3 method for class 'hkmeans'
print(x, ...)

hkmeans_tree(hkmeans, rect.col = NULL, ...)

Arguments

x: a numeric matrix, data frame or vector
k: a single integer specifying the number of clusters to be generated. Must be at least 2 and smaller than nrow(x).
hc.metric: the distance measure to be used. Possible values are "euclidean", "maximum", "manhattan", "canberra", "binary" or "minkowski" (see ?dist).
hc.method: the agglomeration method to be used. Possible values include "ward.D", "ward.D2", "single", "complete", "average", "mcquitty", "median"or "centroid" (see ?hclust).
iter.max: the maximum number of iterations allowed for k-means.
km.algorithm: the algorithm to be used for kmeans (see ?kmeans).
...: others arguments to be passed to the function plot.hclust(); (see ? plot.hclust)
hkmeans: an object of class hkmeans (returned by the function hkmeans())
rect.col: Vector with border colors for the rectangles around clusters in dendrogram

Value

hkmeans returns an object of class "hkmeans" containing the following components:

The elements returned by the standard function kmeans() (see ?kmeans)
data: the data used for the analysis
hclust: an object of class "hclust" generated by the function hclust()

Details

The procedure is as follow:

1. Compute hierarchical clustering

2. Cut the tree in k-clusters

3. compute the center (i.e the mean) of each cluster

4. Do k-means by using the set of cluster centers (defined in step 3) as the initial cluster centers. Optimize the clustering.

This means that the final optimized partitioning obtained at step 4 might be different from the initial partitioning obtained at step 2. Consider mainly the result displayed by fviz_cluster().

Examples

# \donttest{
# Load data
data(USArrests)
# Scale the data
df <- scale(USArrests)

# Compute hierarchical k-means clustering
res.hk <-hkmeans(df, 4)

# Elements returned by hkmeans()
names(res.hk)
#>  [1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
#>  [6] "betweenss"    "size"         "iter"         "ifault"       "data"        
#> [11] "hclust"      

# Print the results
res.hk
#> Hierarchical K-means clustering with 4 clusters of sizes 8, 13, 16, 13
#> 
#> Cluster means:
#>       Murder    Assault   UrbanPop        Rape
#> 1  1.4118898  0.8743346 -0.8145211  0.01927104
#> 2  0.6950701  1.0394414  0.7226370  1.27693964
#> 3 -0.4894375 -0.3826001  0.5758298 -0.26165379
#> 4 -0.9615407 -1.1066010 -0.9301069 -0.96676331
#> 
#> Clustering vector:
#>        Alabama         Alaska        Arizona       Arkansas     California 
#>              1              2              2              1              2 
#>       Colorado    Connecticut       Delaware        Florida        Georgia 
#>              2              3              3              2              1 
#>         Hawaii          Idaho       Illinois        Indiana           Iowa 
#>              3              4              2              3              4 
#>         Kansas       Kentucky      Louisiana          Maine       Maryland 
#>              3              4              1              4              2 
#>  Massachusetts       Michigan      Minnesota    Mississippi       Missouri 
#>              3              2              4              1              2 
#>        Montana       Nebraska         Nevada  New Hampshire     New Jersey 
#>              4              4              2              4              3 
#>     New Mexico       New York North Carolina   North Dakota           Ohio 
#>              2              2              1              4              3 
#>       Oklahoma         Oregon   Pennsylvania   Rhode Island South Carolina 
#>              3              3              3              3              1 
#>   South Dakota      Tennessee          Texas           Utah        Vermont 
#>              4              1              2              3              4 
#>       Virginia     Washington  West Virginia      Wisconsin        Wyoming 
#>              3              3              4              4              3 
#> 
#> Within cluster sum of squares by cluster:
#> [1]  8.316061 19.922437 16.212213 11.952463
#>  (between_SS / total_SS =  71.2 %)
#> 
#> Available components:
#> 
#>  [1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
#>  [6] "betweenss"    "size"         "iter"         "ifault"       "data"        
#> [11] "hclust"      

# Visualize the tree
hkmeans_tree(res.hk, cex = 0.6)

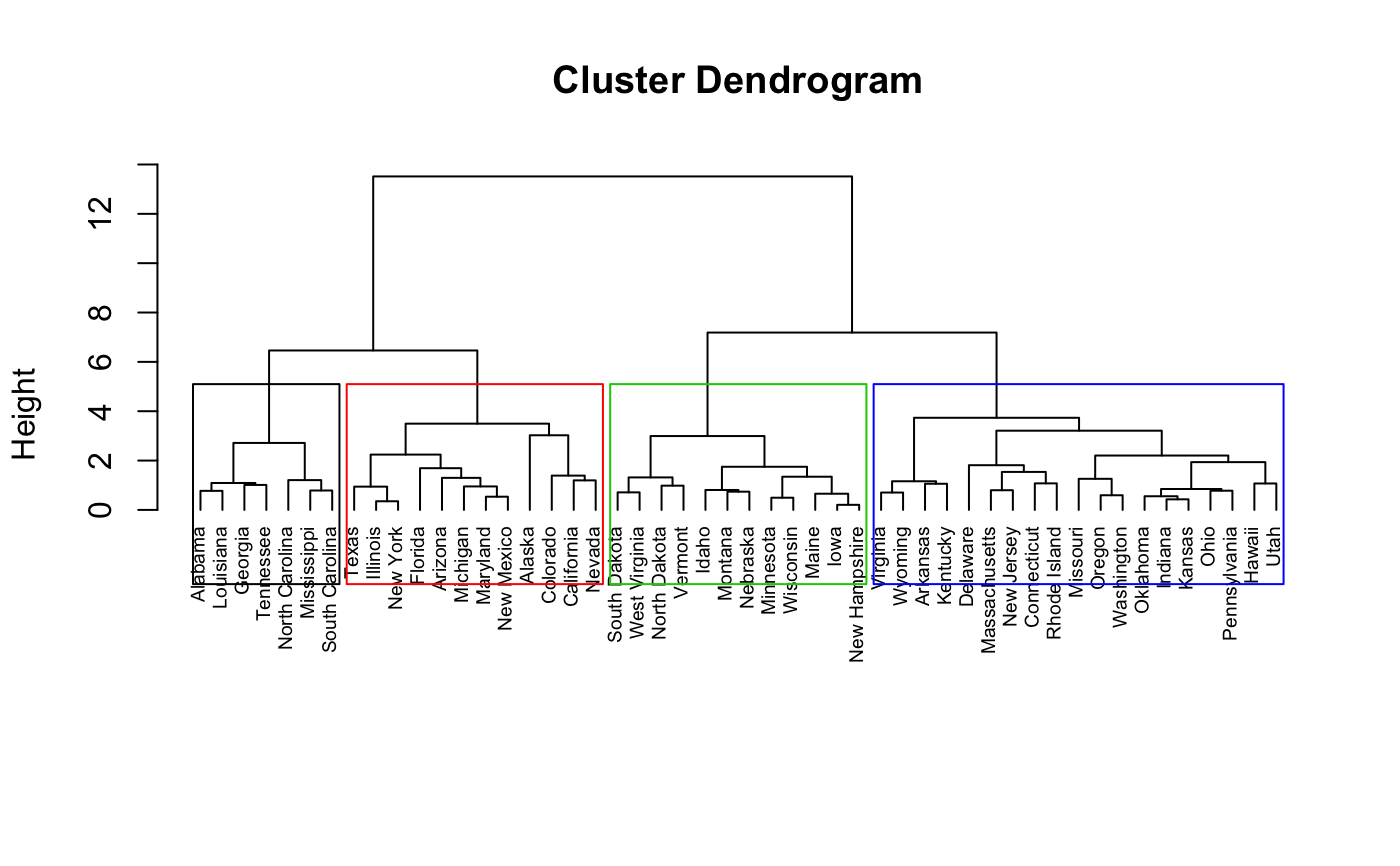# or use this
fviz_dend(res.hk, cex = 0.6)



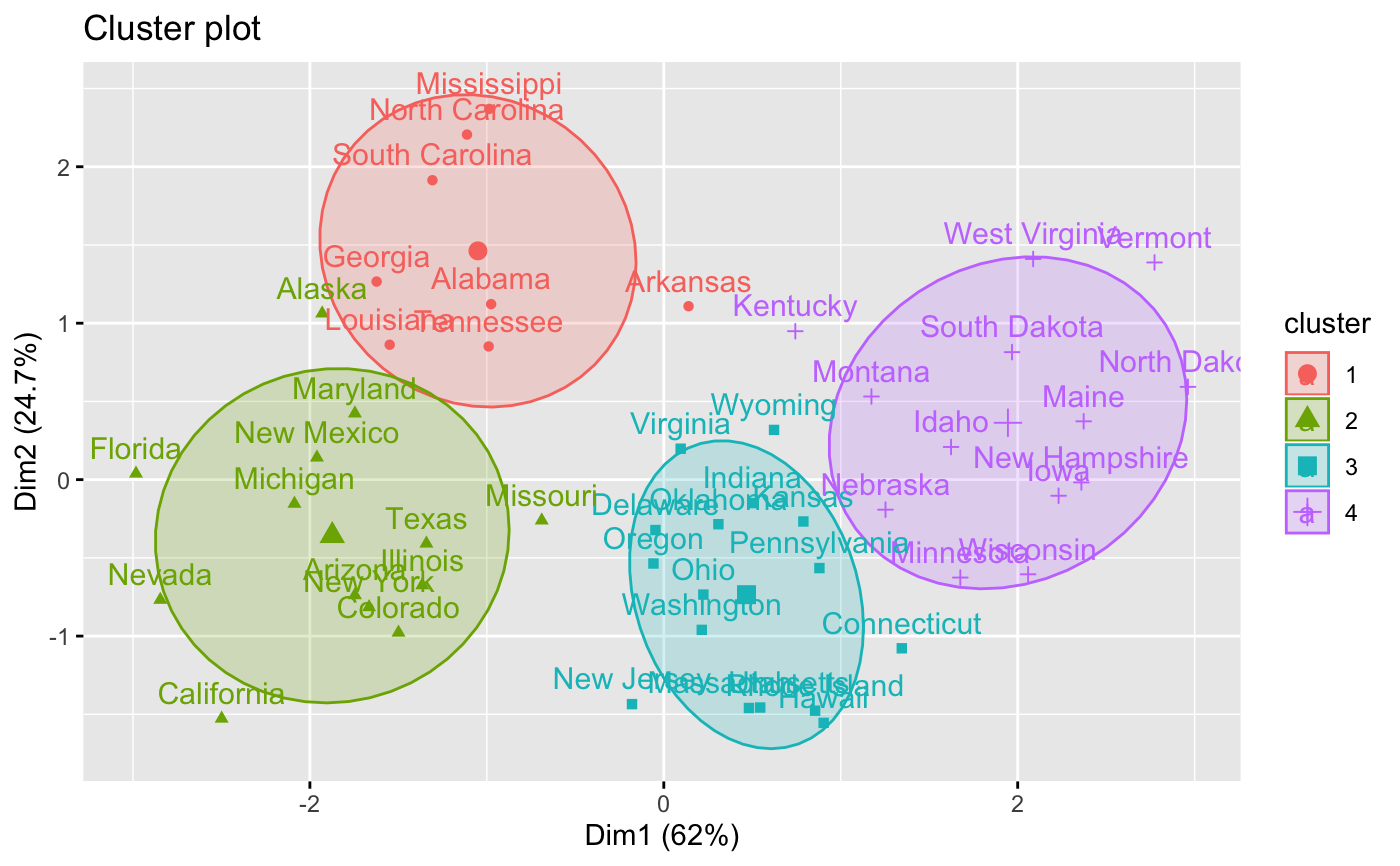
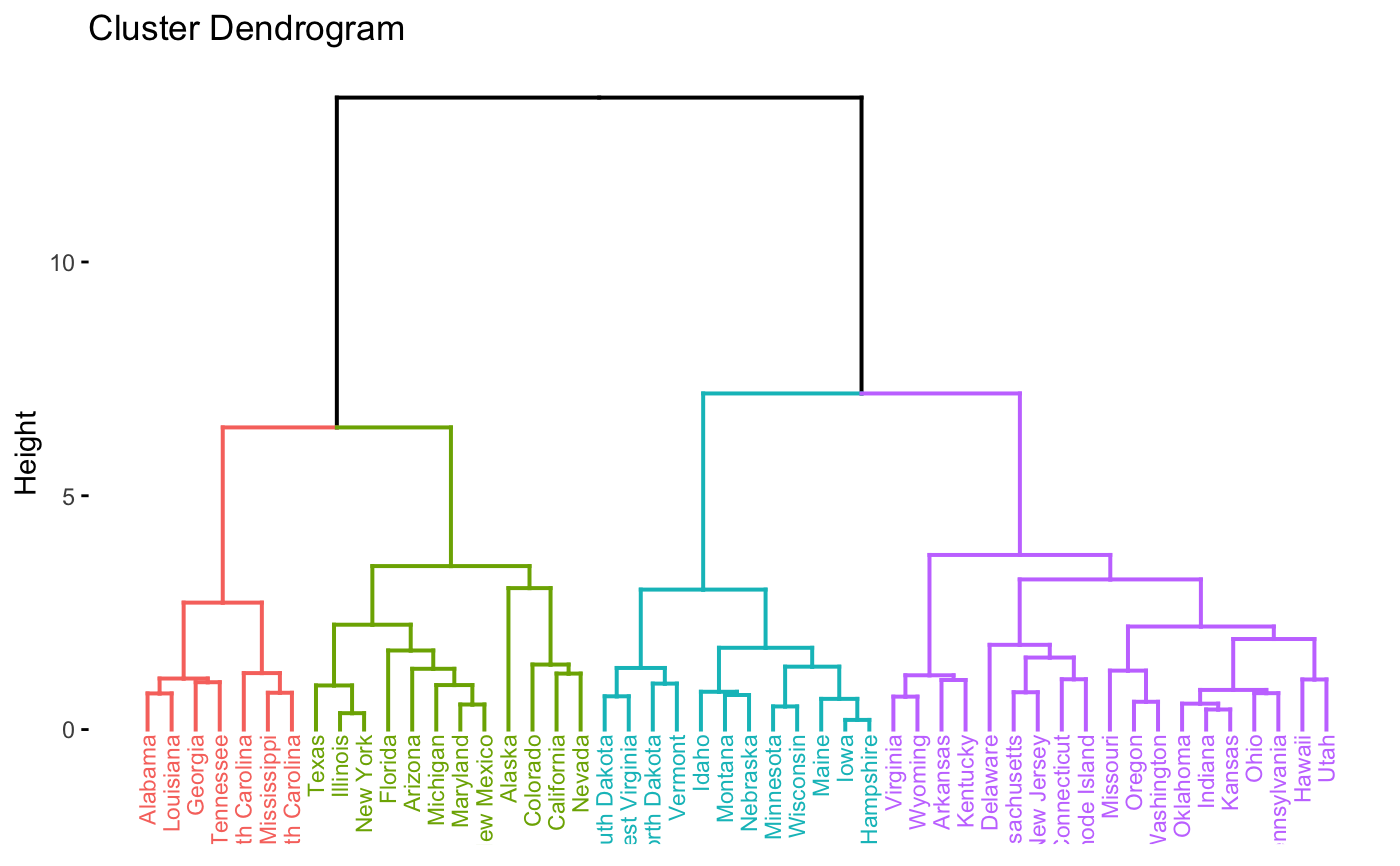# Visualize the hkmeans final clusters
fviz_cluster(res.hk, frame.type = "norm", frame.level = 0.68)
#> Warning: argument frame.type is deprecated; please use ellipse.type instead.
#> Warning: argument frame.level is deprecated; please use ellipse.level instead.

# }